
На примере истории развития математики и геометрии можно проследить путь развития идеи от простого к очень сложному. Геометрия Евклида, Римана, Лобачевского и наконец, Мандельброта. Каждая из упомянутых, произвела революцию в понимании окружающего мира и нашего места в нём, а в совокупности, принесли понимание применимости к той или иной области различных идей и правил.
Наиболее известной из них остаётся, изучаемая в школе, плоская геометрия Евклида, самая доступная в силу своей простоты, наглядности и популярности. Чаще всего её применяют для вычисления различных задач на условной плоскости, но ещё чаще - для наглядности, при представлении различных идей в виде линейных списков, иерархий, типологий и т.п. Например текст это и есть линейное, одномерное, представление мыслей автора. Иерархия - двумерное представление некоей структуры, как и таблица, по сути являя собой проекцию некоего сложного многомерного объекта на линию или плоскость. Читатель воспринимая информацию из такого отображения восстанавливает в своём сознании проекцию до исходной размерности. Окружность и прямоугольник дают возможность предположить что исходным телом был цилиндр.
Всё достаточно просто, до тех пор, пока исходные объекты описываются упрощенной геометрией, в данном случае Евклидовой. Неприятность заключается в том, что в нашем реальном мире, таковой не существует, а проекции из иных, на плоскость перестают быть понятными и тривиальными. Так-же и с пониманием природы сознания и её функции - познания. Описывая столь невероятно сложные объекты с помощью плоских проекций мы теряем возможность воссоздавать исходную структуру. Более того, неправильно выбирая исходную геометрию, мы сужаем возможности нашего познания до примитивного перечисления. Можете представить себе список родового дерева без информации об иерархии?
Мандельброт в своей книге [3] показывает, что к нелинейным системам подобной сложности, такие, как мозг человека, нейронная сеть, и т.п. следует применять иные подходы - геометрию дробных размерностей или иначе говоря геометрию самоподобия (фрактальную) , М.Г. Гапонцева, В.А. Федоров, В.Л. Гапонцев в своей статье [1] и [2] обосновывают применение подобных подходов к моделированию социальных и педагогических теорий.
Данная статья это попытка максимально простым, доступным образом продемонстрировать суть подходов к изучению сложных объектов и понятий на примере описания сути самого процесса познания.
В психологической литературе часто встречается понятие "полярность" как единичный оценочный конструкт или континуум: Хорошо - плохо, свет - тьма, далеко - близко. По всей видимости этот механизм является базовым для функционирования сознания. Впрочем, я бы заменил это понятием "дихотомия". Как определяет википедия : "Дихотоми́я — раздвоенность, последовательное деление на две части, более связанные внутри, чем между собой. Способ логического деления класса на подклассы, который состоит в том, что делимое понятие полностью делится на два взаимоисключающих понятия." - Как видите, сходство есть.
Пример:
"Время суток."
шаг 1 : Свет - тьма.
шаг 2 : Утро - День - Вечер - Ночь
шаг 3 : Раннее утро - Позднее утро - День до обеда - День после обеда - Вечер ранний - Вечер поздний - Ночь до полуночи - Ночь после полуночи.
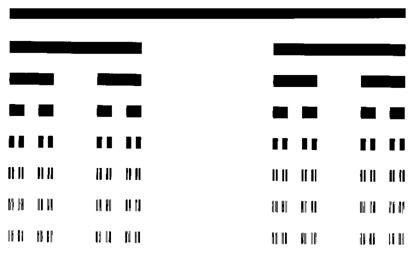
Рис 1. Канторова пыль. Иллюстрация принципа дихотомии.
Можно предположить, что в случае нарушения механизма познания, человек останавливается на первом шаге и дальнейшее изучение явления прекращается. Сообразительный читатель сможет увидеть направление психологической работы, дабы помочь продвинуться клиенту, в случае, когда подобное затруднение является центральным для ситуации, например: оценочные суждения сводятся только к "хорошо-плохо".
Если спроецировать на линию такое представление получится некая фигура (фрактал) с размерностью между 1 и 2. В бесконечности получится множество точек не связанных между собой.
Еще пример:
"Познание"
шаг 1:
неосознанная некомпетентность (не знаю, не умею) - сверхосознанная компетентность (научился и умею учить других)
шаг 2:
неосознанная некомпетентность - Осознанная компетентность (знаю как и учусь уметь) - Неосознанная компетентность (научился и умею) - сверхосознанная компетентность.
В этих простых иллюстрациях, не очевидны преимущества подобных подходов, но это лишь упрощенные примеры, дающие идею для дальнейших, реальных построений моделей сложных структур, таких, как личность и характер.
литература:
1.Журнал "Образование и наука. 2009. №4(61) статья
М.Г. Гапонцева, В.А. Федоров, В.Л. Гапонцев. "Понятия геометрии фракталов как язык объектов педагогики и теории научного знания."
2.Журнал "Образование и наука. 2006. №5(41) статья
М.Г. Гапонцева, В.А. Федоров, В.Л. Гапонцев. "Синергетический подход в педагогической науке:границы и условия применения."
3. Мандельброт Б.Б. Фрактальная геометрия природы. 2002.

